How to win a set: math part

In this post we are going to establish the formula for winning a set given the ability to score a point. We have already derived the formula for winning a game in another post:

$P_{wingame}(x)=x^{4} + 4\cdot x^{4}\cdot(1-x) + 10\cdot x^{4}\cdot(1-x)^{2} + (20\cdot x^{3}\cdot(1-x)^{3})\cdot(\frac{x^2}{2\cdot x^2-2\cdot x + 1})$

We will build on that. In fact, winning a set in tennis means winning 6 or 7 games (either 6-any or 7-5) and occasionally a tiebreak (7-6). We will re-use the formula for winning a game quite often. Therefore, let us create a shortcut and call it $g(x)$ like this:

$g(x):=P_{wingame}(x)$

In order to make the formulas more readable, $x$ will always refer to point winning probabilities, and $y$ will always refer to game winning probabilities.

One can win a set by 6-0, 6-1, 6-2, 6-3, 6-4, 7-5 or 7-6. That leads to this formula:

$P_{winset}(x)=P_{6}(g(x))+P_{75}(g(x))+P_{66games}(g(x))\cdot P_{wintiebreak}(x)$

$P_{6}$ means winning the set with 6 games to 0, 1, 2, 3 or 4 opponent games. $P_{75}$ means winning 7-5, $P_{66games}$ means getting to 6-6, and $P_{wintiebreak}(x)$ means winning the tiebreak.

We are going through exactly the same considerations as in this earlier post.

$P_{6}(y)=\sum\limits_{i=0}^{4} {5+i \choose i}\cdot y^{6}\cdot (1-y)^{i}$

The first part of the above formula states the number of ways of getting to a specific result. For instance, how many ways are there of beating an opponent 6-2? In the above formula this relates to $i=2$ . There are ${7 \choose 2}$ ways of getting to 6-2, because the opponent can win these 2 games anytime before, during or after the first 5 games we score ourselves (but not after the 6th game, because by then, the set would be over).As seen in a previous post, the answer is ${5+2 \choose 2}={7 \choose 2}$ , .

This number is then multiplied by the probability of a single way of getting to a specific result. For instance, one single way of getting to 6-2 has the probability of $y^6\cdot (1-y)^2$ .

The following formulas are of a very similar pattern.

$P_{75}(y)={10 \choose 5}\cdot y^{5}\cdot (1-y)^{5}\cdot y\cdot y={10 \choose 5}\cdot y^{7}\cdot (1-y)^{5}$

$P_{66games}(y)={10 \choose 5}\cdot y^{5}\cdot (1-y)^{5}\cdot y\cdot (1-y)\cdot 2={10 \choose 5}\cdot y^{6}\cdot (1-y)^{6}\cdot 2$

Getting to 6-6 necessarily implies getting to 5-5. The formula uses that fact by first calculating the probability of 5-5, because the first 5 games can be scored in any order (but the sixth game cannot, because it wins the set if the opponent does not already have scored 5 games). The “ $\cdot 2$ ” part is due to the fact that after 5-5 there are two ways of getting to 6-6, i.e. 6-5/6-6 and 5-6/6-6.

$P_{wintiebreak}(x)=P_{7}(x)+P_{66points}(x)\cdot P_{wintiebreakaftersixall}(x)$

The tiebreaker can be won by 7-any or by getting to 6 all and then to win from there by a two point difference.

$P_{7}(x)=\sum\limits_{i=0}^{5} {6+i \choose i}\cdot x^{7}\cdot (1-x)^{i}$

$P_{66points}(x)={12 \choose 6}\cdot x^{6}\cdot (1-x)^{6}$

As opposed to the above $P_{66games}$ , here scoring 6 points does not mean one wins the tiebreak (but winning 6 games wins the set). Thus, the two formulas are not identical.

$P_{wintiebreakaftersixall}(x)=\frac{x^2}{2\cdot x^2-2\cdot x + 1}$

That last part is identical to the formula of winning a game after deuce.

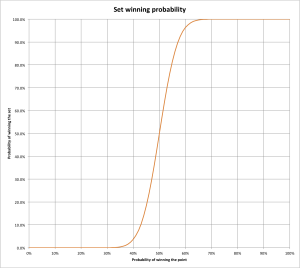
Although we have all the components of the final formula, I will not put its pieces together, as it would just explode. Instead, I will show the resulting graph one more time:

September 15, 2014

Uncategorized Comments are closed Thomas