How to win a game: the math behind

In an earlier post we discussed the probability of winning a game if you know the probability of winning a point. This is the math behind the formula.

The complicated part of the calculation is that a game of tennis can go over deuce many times, even indefinitely (in theory, at least). We will therefore treat the deuce part and the no-deuce part separately.

Mathematically speaking, the probability of winning a game is the probability of winning without deuce $P_{winnodeuce}$ plus the probability of winning with deuce $P_{windeuce}$ (since these are disjoint events).

$P_{wingame}(x)=P_{winnodeuce}(x)+P_{windeuce}$

Recall that $x$ is the probability of winning a single point. $P_{winnodeuce}(x)$ consists of winning the point after 40-0, 40-15 or 40-30. The question now is how many ways of getting to 40-0, 40-15 or 40-30 are there? The first one (40-0) is easy, there is only one way: 15-0, 30-0, 40-0. The second one is more difficult, as there are already 4 different ways: (1) 15-0, 30-0, 40-0, 40-15, (2) 15-0, 30-0, 30-15, 40-15, (3) 15-0, 15-15, 30-15, 40-15, and (4) 0-15, 15-15, 30-15, 40-15.

Generally, this kind of problem is known as the number of possible selections of $k$ elements amongst a set of $n$ elements, written as ${n}\choose{k}$ . In the context of our problem, $n$ is the number of points played and $k$ is the number of points your opponent scores. Equivalently, $k$ can be seen as the number of points you will score, which is always $3$ (you need $3$ points to reach 40-?). So there are ${n}\choose{3}$ ways of reaching 40-?. The interpretation is that in a series of $n$ points played, you can select any $3$ points among them in order to get to 40-?.

The probability of e.g. winning the game after 40-15 is $x$ times the probability of reaching 40-15. The probability of reaching 40-15 is ${{4}\choose{3}}\cdot x^{3}\cdot (1-x)^{1}$ , as you have to score $3$ points ( $x^{3}$ ) and your opponent scores one point ( $(1-x)^{1}$ ). So winning after 40-15 is as probable as $x\cdot {{4}\choose{3}}\cdot x^{3}\cdot (1-x)^{1}$ .

Putting it all together for the three different cases (40-0, 40-15, 40-30), we get

$P_{winnodeuce}(x)=x\cdot {{3}\choose{3}}\cdot x^{3}+x\cdot {{4}\choose{3}}\cdot x^{3}\cdot (1-x)^{1}+x\cdot {{5}\choose{3}}\cdot x^{3}\cdot (1-x)^{2}$ . Simplified, this is

$P_{winnodeuce}(x)={{3}\choose{3}}\cdot x^{4}+{{4}\choose{3}}\cdot x^{4}\cdot (1-x)+{{5}\choose{3}}\cdot x^{4}\cdot (1-x)^{2}$ and

$P_{winnodeuce}(x)=1\cdot x^{4}+4\cdot x^{4}\cdot (1-x)+10\cdot x^{4}\cdot (1-x)^{2}$

We have got part one of $P_{wingame}(x)$ . Part two has two main components, the probability of getting to deuce ( $P_{gettodeuce}(x)$ ) and the probability of winning at deuce ( $P_{winatdeuce}(x)$ ). In order to get $P_{windeuce}(x)$ , these two components can simply be multiplied ( $P_{windeuce}(x)=P_{gettodeuce}(x)\cdot P_{winatdeuce}(x)$ ).

The probability of getting to deuce is $P_{gettodeuce}(x)={{6}\choose{3}}\cdot x^{3}\cdot(1-x)^{3}$ , as $6$ points have to be played, $3$ of which either player has to win (this is the number of ways getting to 40-40) times the probability of winning three points each ( $x^{3}$ , $(1-x)^{3}$ respectively).

The probability of winning a game at deuce is a function of winning two points in a row, plus winning only one point each (which is deuce again) and winning the game from there. This is the formula: $P_{winatdeuce}=x^{2} + 2\cdot x\cdot (1-x)\cdot P_{winatdeuce}$ . This resolves to $P_{winatdeuce}=\frac{x^2}{2\cdot x^2-2\cdot x + 1}$ .

We get

$P_{windeuce}(x)={{6}\choose{3}}\cdot x^{3}\cdot(1-x)^{3}\cdot \frac{x^2}{2\cdot x^2-2\cdot x + 1}=20\cdot x^{3}\cdot(1-x)^{3}\cdot \frac{x^2}{2\cdot x^2-2\cdot x + 1}$

Putting it all together, we get the formula we have been looking for:

$P_{wingame}(x) = x^{4} + 4\cdot x^{4}\cdot(1-x) + 10\cdot x^{4}\cdot(1-x)^{2} + (20\cdot x^{3}\cdot(1-x)^{3})\cdot(\frac{x^2}{2\cdot x^2-2\cdot x + 1})$

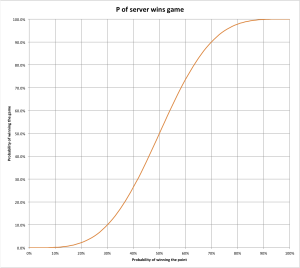
For ${0}\leq{x}\leq{1}$ , the function plots like this:

June 29, 2014

Math & Physics Understand Comments are closed Thomas