Can You Hold Serve?

Would you like to know how you can hold serve more often? Then, this post is for you.

In tennis, with the advantage of the serve you should usually win the point. Not only can you hit the serve without interference from your opponent, you have even got two shots at it! With that much of an advantage, to win the point when serving should be easy. Often though, at a recreational level, it is not.

There are two types of counterforce at work: one is psychological, the other mathematical. The psychological counterforce is that your opponent does matter, even if she is not influencing your serve physically. You know that your serve will be returned by that particular opponent of yours. A weak serve might be okay against a weak opponent, but it spells trouble against a strong opponent. When facing a strong opponent, you might push your serve to the limit and beyond. Thus, your serve is influenced by the opponent, although not in a physical manner.

The mathematical counterforce has to do with the order of hitting the ball. To serve means to hit the ball first. From a mathematical point of view, hitting the ball should be generally avoided, because there is a chance of immediately losing the point. The ball can go out or fly into the net. Thus, to serve means to attempt a shot before the opponent has to. This is a bad thing, even if you have two attempts available, because you can fail twice. Failing twice is a double-fault. That means there is a chance of losing the point without giving the opponent a chance of faulting. Mathematically speaking, this considerably lowers your chances of winning the point.

Now let’s assume that serving gives you an edge over your opponent. Have you ever wondered how likely it is you will win the game? Say you have a 60% chance of winning the point when serving. What is your chance of winning the entire game? With a little help of combinatorics we can answer that question.

If $x$ is your probability of winning the point when at serve, then, this is the probability of winning the game:

$P_{game}(x) = x^{4} + 4\cdot x^{4}\cdot(1-x) + 10\cdot x^{4}\cdot(1-x)^{2} + (20\cdot x^{3}\cdot(1-x)^{3})\cdot(\frac{x^2}{2\cdot x^2-2\cdot x + 1})$

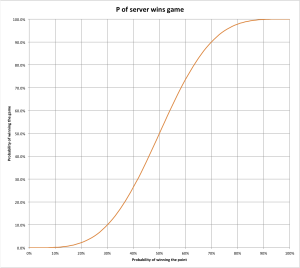
The function plots like this:

We dig into the math in another post. Let us focus on the curve instead. It has a steepness of around 2 between 50% and 70%. This is very cool, as it means for every percentage increase you will be rewarded double that amount. For instance, if you increase your point winning percentage by 5%, your game winning percentage will rise 10%. Similarly, if you manage to increase point win percentage by 10%, you will increase game win percentage by 20%. As mentioned, this holds roughly true between 50% and 70%. For instance, if you increase your serve points percentage from 50% to 55%, you will win 60% of your games instead of only 50%. This means you win 20% more games! ( $\frac{0.6-0.5}{0.5}=0.2$ )

Can you hold serve? It depends on your point winning percentage. Summing up, these are two recommendations:

Do not push your serve beyond its limit. Do not double-fault.
Increase the effectiveness of your serve. You will be generously rewarded.

June 26, 2014