Given your ability to win a single point in tennis, how likely is it you will win the set? If you want to win 9 out of 10 sets, by what margin do you need to dominate your opponent?
It turns out that the answer is 4 out of 7 points. That’s right! You only need to score 4 out of 7 points (=57%) on average! Then you already win 9 out of 10 sets. Symmetrically, winning only 3 out of 7 points leads to losing 9 out of 10 sets.
Let us give some other examples. Say you score 5 out of 8 points (=62.5%) on average. This already leads you to winning 79 out of 80 sets! By the time you manage to score 2 out of 3 points (=66.6%), you will win 699 of 700 sets. Incredible, isn’t it?
This makes tennis a cruel game. Lose slightly more points than your opponent, and you will almost certainly lose the set. Why is this?
It is twofold. First and foremost, repeating a deal at which one has a disadvantage is generally a bad idea. But this is exactly what tennis is about! Point after point is repeated until the disadvantage becomes apparent. Second, the structure of tennis with its points, games, and sets is increasing the disadvantage even further. It is not enough to score three points (e.g. 40-0), they are worthless if one does not manage to score the fourth point which brings home the game. If a tennis set was structured like a big single tiebreak (going to 24 points), the disadvantage would be less. Take the example above. Winning only 3 out of 7 points would normally lead to losing 9 out of 10 sets. In the big tiebreak version, one would lose only 8.5 out of 10 sets.
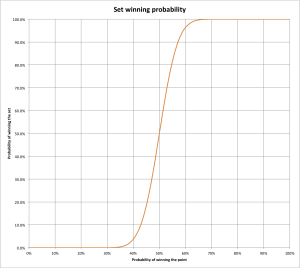
Here is the plot showing the full cruelty of tennis:
We will dig into the math details in another post.
Look at that graph. On the x-axis is the ability to win a single point. On the y-axis you can see the resulting probability of winning the set.
For example, if you have the ability to score 50% of the points, then obviously you will win 50% of the sets. If you score 60% of the points, the graph shows more than a 95% set winning probability. From 65% onwards, winning the set is almost certain.
Seeing all this clashes a little bit with reality. Isn’t it the case that most matches are much tighter than this graph would predict?
Yes and no. Yes, because the whole consideration is only theoretical in nature. It assumes a constant point winning ability. This is not realistic for two reasons. First, there are serve games and there are return games. The server is usually at an advantage, so the advantage/disadvantage pattern switches every game. Second, there is psychology. For instance, players tend to get a re-break right after they have broken their opponent.
And no, because we can observe many matches with very clear results. In these matches we can see very able professionals losing clearly despite them dominating many points.
How to win a set? The answer is both simple and frustrating: Have a tiny little edge over your opponent! The good part is that the edge only needs to be tiny. The bad part is that you desperately need it. And you need it consistently over the whole set and match.

https azino 777
azino777 бонус 777 рублей без депозита
супер слотс бездепозитный бонус 500
super slots casino отзывы
играм на сайте vavada
скачать vavada на андроид
pin up casino скачать бесплатно
pin up casino официальный сайт 2020
sol casino официальный сайт скачать
сол казино скачать
казино фараон онлайн играть бесплатно автоматы
казино фараон сорвать куш
плей фортуна на андроид
казино play fortuna отзывы
казино слот в сайт
слот в казино вход
скачать мобильный покердом
poker dom скачать
vulkan slots мобильная версия
вулкан slots россия
клевый веб ресурс
Ню фото голых телок раком
you can try here https://hydramirror2020.com
I don’t ordinarily comment but I gotta state thanks for the
post on this one :D.
Also visit my page: exams
Hi friends, pleasant piece of writing and pleasant arguments commented here, I
am in fact enjoying by these.
Feel free to visit my blog: exams
come perdere la pancia
https://visasam.ru/emigration/pereezdsng/grazhdanstvo-moldovy.html
http://shopinweb.ru
can using viagra make you impotent whathappens when women consume viagra viagra tumblr
Guys just made a web-site for me, look at the link:
https://www.google.com/url?sa=t&url=http%3A%2F%2Fvmirezdorovya.ru/polza-ispolzovaniya-serebryanoj-posudy/ Tell me your references. THX!
казино х играть онлайн россия
обзор казино икс
Bamboo Premium Plush Mattress Protector – Soft, Quiet, Comfortable topper, cover – Hypoallergenic, Deep Fitted Pocket (Twin Size)
Bedtime Originals Magic Garden Pink/White Butterfly Lamp with Shade & Bulb
Guys just made a web-site for me, look at the link:
https://planland.godaddysites.com/ Tell me your references. Thanks!
Препараты качественные,купили на сайте anticancer24.ru
Доставили из Москвы за 3 дня
софосбувир +и даклатасвир цена +в челябинске 2019
LS-0153 Short Sleeve Bodysuit – Red, Newborn – Pack of 5
Dimple 50 Piece Die Cast Metal Vehicles City Set
рокс казино скачать
rox casino приложение скачать
Hi! get lasix online buy lasix in us
check this link right here now hydra
яндекс директ промокод купить – скидка яндекс директ, купить купон на яндекс директ
вывод из запоя стоимость – лечение женского алкоголизма в домашних условиях, лечение алкогольной зависимости
азино три топора игра
azino777 форум
look at this now empire dark web market
this article empire market mirror
русский егэ репетитор – репетитор по русскому языку в спб, курсы егэ
Установка распределительных коробок защищает провода от случайного повреждения. Материал с сайта electrotorg.ru
College Girls Porn Pics
http://jsutandy.com/?mallory
police porns shana evans porn forum free public invasion porn avatar last air bender porn games husband porn addicted
центр лечения алкогольной зависимости – цена кодировки от алкоголизма, где можно закодироваться от алкоголизма
неплохой ресурс
https://sexreliz.net/anal/687-otodral-zasranku-v-dymohod.html
see this empire market onion
go to these guys dark web
достохвальный вебсайт
https://sexreliz.net/treason/1805-tetrad-najdennaja-na-bolote-u-krasnyh-holmov.html
https://newsmaker.md/rus/novosti/kak-bystro-i-legalno-poluchit-grazhdanstvo-moldovy-emigraremd-znaet-otvet/
American Red Cross Premium Comfort Careв„ў Nursery Kit
Lillian Rose Noah’s Ark Pewter Bank
anvelope-moldova.md
Препараты качественные,купили на сайте anticancer24.ru
Доставили из Москвы за 3 дня
софосбувир +и даклатасвир лечение цена
актуальный вход казино pin up
pin up casino Р±РѕРЅСѓСЃ
come dimagrire
Препараты качественные,купили на сайте anticancer24.ru
Доставили из Москвы за 3 дня
купить софосбувир +и даклатасвир цена 2019