Spin calculation

The last post made several claims about topspin production. In this post, we will explore the physics behind them.

Recall the illustrative picture of a tennis great from the last post:

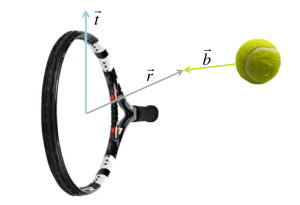
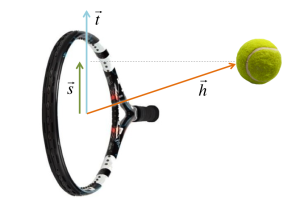
We can draw the same arrows in a more abstract manner like this:

In order to make things easy, we will always draw that picture with the blue arrow pointing straight up to the sky (i.e. the racquet has no tilt). If there is racquet head tilt (as in the Federer picture above), we just rotate the whole picture. We can do so without losing generality because gravity does hardly affect spin production at all.

So let us name three vectors as follows. Let

$\vec{b}$ be the vector of the incoming ball (yellow arrow),

$\vec{r}$ be the vector of the racquet movement measured at the point of ball impact (grey arrow),

$\vec{t}$ be the tilt of the racquet face (blue arrow) with $|\vec{t}|=1$ by definition. The racquet tilt vector is on the same plane as the racquet. It simply measures how much the racquet is tilted forward (topspin) or backward (slice).

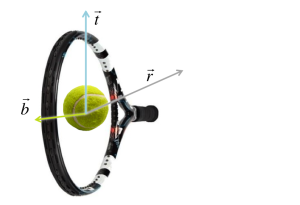
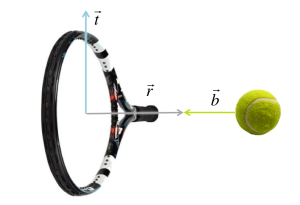
Side note: For the sake of better illustration, the above picture is drawn as if it was before ball impact. But it is not. Actually, our consideration is at the moment of ball impact, like this:

We just drew the same vectors at a different position, which does not change anything, as vectors are position agnostic.

Second side note: Yes, the vectors in the Federer picture are derived from frames before ball impact, which is actually wrong, but it is the best estimate of the velocities & angles at ball impact I could come up with. The assumption is that both the ball vector and the racquet vector do not change very much during the very short time between the two video frames.

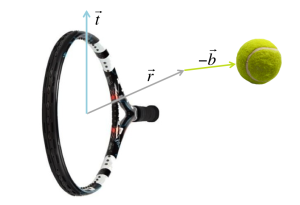
In physics, it helps to choose an appropriate reference system. Currently, we are looking from the outside (the world!). With the world as a reference system, both the racquet and the ball are moving, which makes it harder for us to conclude anything. Let us choose the incoming ball as reference system. That way, at least the ball will be steady.

This means we will pretend there is a tiny camera placed on the ball surface from which we will look at everything. In order to get the ball steady, we need to subtract $\vec{b}$ from the racquet and the ball. The ball will then stand still ( $\vec{b}-\vec{b}=0$ ), and the racquet will move with an additional $-\vec{b}$ . The picture now looks like this:

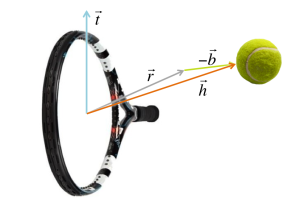
Which results in the orange overall racquet movement vector:

In our new reference system, the racquet head moves with $\vec{h}=\vec{r}+(-\vec{b})=\vec{r}-\vec{b}$ toward the steady ball.

Now the spin $\vec{s}$ on the ball is simply the velocity of the racquet at ball impact location in tangential direction. That tangential direction happens to be $\vec{t}$ . So we are looking for $\vec{s}$ (the spin vector) and we already know its direction, which is $\vec{t}$ . Thus, we need to look for $|\vec{s}|$ , the length of $\vec{s}$ .

According to vector calculations, and specifically to scalar projection, $|\vec{s}|=\vec{h}\cdot \vec{t}$ . Resolving back $\vec{h}$ yields $|\vec{s}|=|(\vec{r}-\vec{b})\cdot \vec{t}|$ .

Now as we can see, spin production is directly proportional to the scalar product of $\vec{h}$ and $\vec{t}$ . The scalar product is nothing but the cosine of the angle between $\vec{h}$ and $\vec{t}$ times the length of $\vec{h}$ (the length of $\vec{t}$ is one by definition).

The cosine of the angle between $\vec{h}$ and $\vec{t}$ is zero if the two vectors are orthogonal. This means if both the ball and the racquet move horizontally and there is no racquet tilt, then there is no spin at all.

From there, tilting the racquet a bit immediately yields spin production. The same holds true for moving the racquet upward. Neglecting ball speed, both tilting the racquet and moving the racquet upward are symmetrical with regard to spin production. This means increasing the racquet upward movement angle by 1 degree yields the same spin increase as tilting the racquet head forward by 1 degree.

However, with regard to ball trajectory, the two are completely different. Tilting the racquet forward makes the ball fly lower over the ground. Moving the racquet head more upward results in a higher ball trajectory, which is quite the opposite. A nice blend of both will result in a reasonable ball trajectory with very much spin on the ball.

In the next posts, we will look at how one can produce topspin with more consistency, and why it is beneficial to tilt the racquet forward.

August 8, 2014